Answer:-
Free online cuboid calculator – Enter the cuboid length, width and height then click the calculate button.
What is a Cuboid?
A cuboid, also known as a rectangular prism, is a three-dimensional geometric shape with six rectangular faces, twelve edges, and eight vertices.
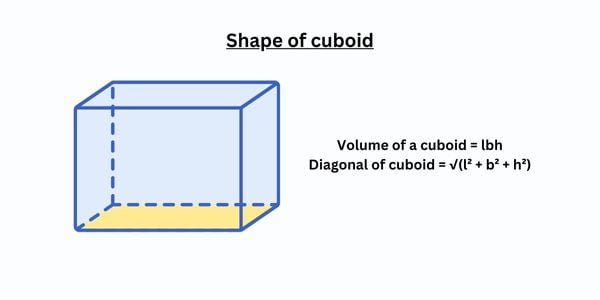

Cuboid formula
- Volume of a cuboid = lbh
- Diagonal of cuboid = √(l² + b² + h²)
- Curved/Lateral Surface Area = 2(lh + bh)
- Total Surface Area = 2(lh + bh + lb)
- Where l-length, b-breadth,h-height
Solved example
Example.:- A room has 16m length, 14m breadth and 7m height then find its volume of room and surface area of the room.
Answer => l→ 16 m, b→ 14 m, h→ 7 m
Volume = lbh = (16 x 14 x 7) m³ = 1568m³
Total Surface Area = 2(lh + bh + lb) = [2(16 x 14 + 14 x 7 + 16 x 7)] cm² = (2 x 434) cm² = 868 cm²